В стереометрии наряду с задачами на доказательство и вычисление решаются задачи на построение, но подход к методике изучения несколько иной, чем в планиметрии.
Задачи на построение в пространстве решаются двумя методами:
1) Задачи на воображаемое построение или задачи на доказательство существования фигур;
2) Задачи на проекционном чертеже.
В процессе решения задач на построение в воображении устанавливается лишь факт существования решения, само же построение искомого элемента не выполняется. По идее метода элементы, определяемые условием задачи, не задаются непосредственно в пространстве, ни на плоском чертеже, а удерживается в воображении. Решение задачи сводится к перечислению такой совокупности геометрических операций, фактическое выполнения которых (в случае если их можно было выполнить) приводит к построению искомого элемента. Задача считается решенной, если удается отыскать рассматриваемую совокупность построений.
При выполнении «воображаемых» построений считаем, что, во-первых, умеем строить плоскость, если заданы определяющие ее элементы (три точки, не лежащие на одной прямой, или прямая и точка вне ее, или две пересекающиеся прямые, или две параллельные прямые), и, во-вторых, в любой плоскости умеем осуществить все те построения, которые обоснованы в планиметрии. Так, если требуется провести через данную прямую а произвольную плоскость, берут произвольную точку А вне прямой а (возможность выбора такой точки также постулируется) и считают, что искомая плоскость проведена через прямую а и точку А.
Проиллюстрируем прием решения задач на построение в воображении на примере решения следующей задачи.
Задача 1. Построить плоскость, параллельную данной плоскости
b
и проходящей через данную точку В
Решение. Допустим, что точка В не лежит в плоскости b. Решение задачи в этом случае свелось бы к перечислению следующей совокупности построений:
1) в плоскости b проводим две пересекающиеся прямые a и b;
2) через прямую а и точку В проводим плоскость g1;
3) в плоскости g1 через точку В проводим прямую a1, параллельную прямой а;
4) через прямую b и точку В проводим плоскость g2;
5) в плоскости g2 через точку В проводим прямую b1, параллельную прямой b;
6) через две пересекающиеся прямые a1 и b1 проводим плоскость b. плоскость b¢– искомая.
Чертеж при решении в воображении задач на построение может не выполняться. В тех же случаях, когда к нему прибегают, он играет вспомогательную роль: чертеж необходим только для облегчения работы воображения, когда пространственное воображение плохо развито или когда построения оказываются громоздкими.
В учебнике такие задачи решаются в разделах параллельные и перпендикулярные прямые и плоскости в пространстве в 10 классе, и большинство из них даны с решением (чаще всего просто построение, без анализа, доказательства, без исследования).
При решении задач на построение на проекционном чертеже элементы, определяемые условием задачи, задаются на изображении оригинала (точки, линии, плоскости, геометрические тела пространства в любой из материальных реализаций или воображаемые). Для эффективного решения задач на построение используются полные изображения, построение на которых выполняются без какой бы то ни было степени произвола.
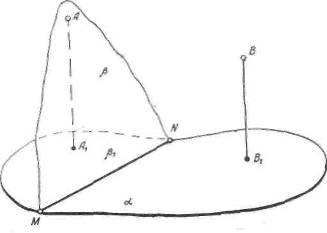 |
Рис. 1
Решение. Элементы, определяемые условием задачи, задаются на изображении так, как это выполнено на рисунке 1:
В плоскости b(b1) строим АМ (А1М) и AN (А1 N). В соответствии с условиями проекционного чертежа прямые АМ (А1М) и AN (А1 N) служат прямыми, принадлежащими плоскостиb(b1). C помощью линейки и угольника проводим через прямые BN1 (B1N1) и BM1 (B1M1), параллельные прямым АМ (А1М) и AN (А1 N). Такие прямые строятся единственным образом и действительно изображают прямые, параллельные прямым АМ (А1М) и AN (А1 N). Пересекающиеся прямые BN1 (B1N1) и BM1 (B1M1) определяют искомую плоскость b¢.